快速排序

快速排序概念：快速排序由C. A. R. Hoare在1962年提出。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

递归实现快速排序

原数组：

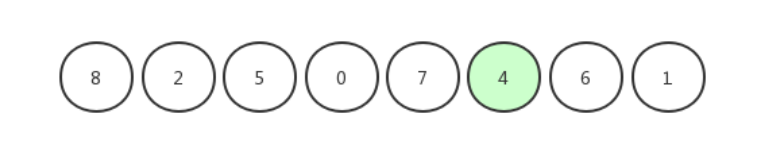
快速排序最重要的一个过程是：使用原数组中的随机一个数基准，它能够把数组划分为左右两部分的数，比基准小的数都在其左边，比基准大的数都在其右边。这个划分数组的过程称作partition，划分后的数组：

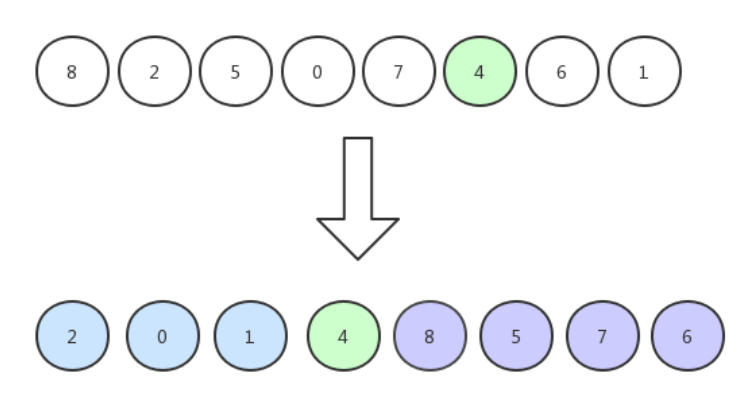
挖坑法来处理partition的划分过程：

首先先取数组的最左边第一个值作为基准，用一个变量记录下基准的值，设置left和right指针，分别指向数组的最左边和数组的最右边。第一步，先从数组最右边开始查找第一个比基准小的数，当然，如果都比基准大，则right指针在不小于left指针的情况下，不断往左移。当right指针找到第一个比基准小的值时，覆盖掉left指针所在位置，因为我已经记录了数组中第一个位置的值，因此直接交换也没有问题。

然后我们以同样的方式排左边的数据：

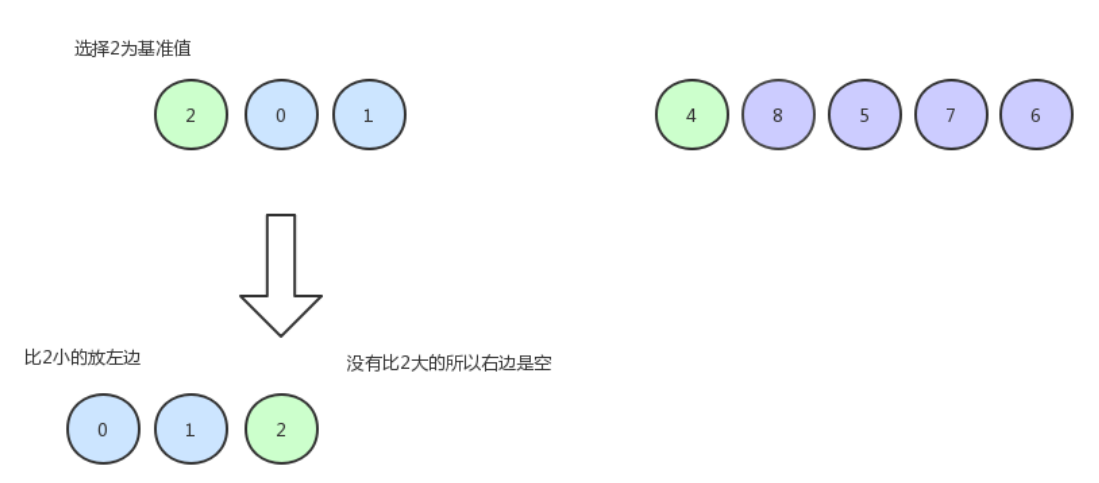
以相同的方式继续排 0 和 1 ：

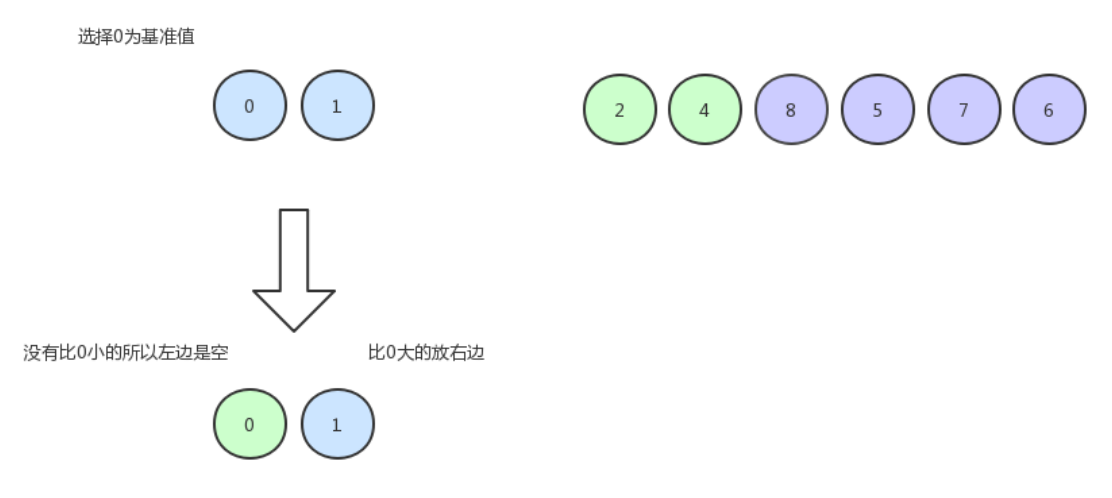
由于只剩下一个数，所以就不用排了，现在的数组序列是下图这个样子，可以看到 4 这个基准排到了它最终应该所处在的一个位置：

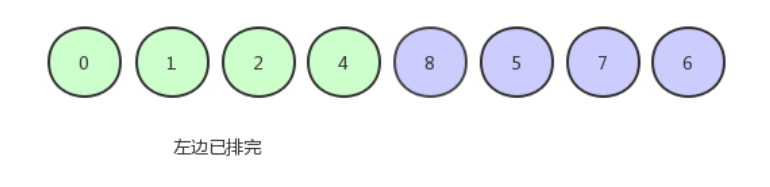
此时基准就放到了它最终应该所处的位置，再把基准左边和右边的子数组递归地进行上述操作，最终整个数组一定是有序的。

递归实现快速排序代码实现如下：

public class QuickSort {
    //快速排序递归
    public static void quickSort(int[] arr,int left,int right) {
        if(left>=right) {
            return;
        }
        int pivot = partition(arr,left,right);
        quickSort(arr,left,pivot-1);
        quickSort(arr,pivot+1,right);
    }

    private static void swap(int[] arr, int midValIndex, int left) {
        int tmp = arr[midValIndex];
        arr[midValIndex]=arr[left];
        arr[left]=tmp;
    }

    private static int partition(int[] arr, int low, int high) {
        int tmp = arr[low];
        while(low<high) {
            while(low<high&&tmp<=arr[high]) {
                high--;
            }
            arr[low]=arr[high];
            while(low<high&&tmp>=arr[low]) {
                low++;
            }
            arr[high]=arr[low];
        }
        arr[low]=tmp;
        return low;
    }
}

快速排序的最好时间复杂度为O(N*log^N)，是在基准能够平均划分数组的前提下才能达到。最坏时间复杂度为O(N^2)，是在基准一个数都没有划分在其右边或左边的情况下达到。空间复杂度为O(log^N)，因为递归是会开辟栈空间的，此时最好的空间复杂度即树的高度（可以将基准划分后的左右两边看成子树，基准为根），最坏空间复杂度为O(N)，即可以看作一个链表，数组原本是从大到小排序的。

上面快速排序的递归，是没有经过优化的。经过优化的快速排序的递归有：

1. 在数组的大小没有超过60的情况下，最好使用插入排序进行处理，虽然插入排序的时间复杂度为O(N^2)，但是在常数规模上，是优于快速排序的。
2. 三数取中法。此时有一个问题，如果直接选数组中最左边的数作为基准，假设这个基准是最大的或者最小的，就很有可能起不到划分数组的作用，因此可以把数组的最左、最右、中间的数比较，取中间大的那个数作为基准，进行partition过程。

对上面的三数取中法，可能会有小伙伴会感到疑惑。举个例子：当一个数组由[6，5，4，3，2，1]组成（待排序的序列为正序或者逆序，都会造成最坏的时间复杂度），假设此时直接用快速排序对数组进行排序，则时间复杂度为O(N^2)。最坏时间复杂度的快排的递归表达式如下：T(n)=T(n-1)+O(n)

知道这组无序数列的首和尾后，我们便可以求出这个无需数列的中间位置的数，我们只需要在首，中，尾这三个数据中，选择一个排在中间的数据作为基准值，进行快速排序，即可进一步提高快速排序的效率。那么为什么要取中间呢？我们可以假设待排序的数列是一组高度有序的数列，显然首极大可能是最小值，尾极大可能是最大值，此时如果我们选取一个排在中间的值，哪怕是在最坏的情况下，left和right只需要走到中间位置，那么这个中间值的位置也就确定下来，而不需要left或right指针要把整个数列遍历一边，从而大大提高快速排序的效率。底下的SelectThreeMid方法则是三数取中法。

递归实现快速排序代码如下：

public class QuickSort {
    //快速排序递归
    public static void quickSort(int[] arr,int left,int right) {
        if(left>=right) {
            return;
        }
        if(right-left+1<=1400) {
            insertSort2(arr,left,right);
            return;
        }
        int midValIndex = SelectThreeMid(arr,left,right);
        swap(arr,midValIndex,left);
        int pivot = partition(arr,left,right);
        quickSort(arr,left,pivot-1);
        quickSort(arr,pivot+1,right);
    }

    private static void swap(int[] arr, int midValIndex, int left) {
        int tmp = arr[midValIndex];
        arr[midValIndex]=arr[left];
        arr[left]=tmp;
    }

    private static void insertSort2(int[] arr,int start,int end) {
        for(int i=1;i<=end;i++) {
            int j=i-1;
            int tmp = arr[i];
            for (; j >=start ; j--) {
                if(arr[j]>tmp) {
                    arr[j+1]=arr[j];
                }else {
                    break;
                }
            }
            arr[j+1]=tmp;
        }
    }

    private static int SelectThreeMid(int[] arr,int left,int right) {
        int mid = left+((right-left)>>>1);
        if(arr[left]<arr[right]) {
            if(arr[mid]>arr[right]) {
                return right;
            }else if(arr[left]>arr[mid]) {
                return left;
            }else {
                return mid;
            }
        }else {
            if(arr[mid]>arr[left]) {
                return left;
            }else if(arr[right]>arr[mid]) {
                return right;
            }else {
                return mid;
            }
        }
    }

    private static int partition(int[] arr, int low, int high) {
        int tmp = arr[low];
        while(low<high) {
            while(low<high&&tmp<=arr[high]) {
                high--;
            }
            arr[low]=arr[high];
            while(low<high&&tmp>=arr[low]) {
                low++;
            }
            arr[high]=arr[low];
        }
        arr[low]=tmp;
        return low;
    }
}

非递归实现快速排序

思路：快速排序非递归要用到栈。首先要了解递归过程的实质，它其实是在内存中开辟出递归栈，记录递归的上下文。此时非递归就是使用栈来模拟出递归栈在递归中的用途。partiton过程不变。当然，如果基准的下标一定要大于start+1或者end-1才有意义，因为如果等于start+1(end-1同理)则证明需要划分的子数组长度为2，就没有划分数组的必要了。

非递归实现快速排序如下：

    public static int partition(int[] arr,int low,int high) {
        int tmp = arr[low];
        while(low<high) {
            while(low<high&&tmp<=arr[high]) {
                high--;
            }
            arr[low]=arr[high];
            while(low<high&&tmp>=arr[low]) {
                low++;
            }
            arr[high]=arr[low];
        }
        arr[low]=tmp;
        return low;
    }
    public static void quickSort(int[] array) {
        Stack<Integer> stack = new Stack<>();
        int start = 0 ;
        int end= array.length-1;
        int pivot = partition(array,start, end);
        if(pivot>start+1) {
            stack.push(0);
            stack.push(pivot-1);
        }
        if(pivot<end-1) {
            stack.push(pivot+1);
            stack.push(end);
        }
        while(!stack.empty()) {
            end =stack.pop();
            start =stack.pop();
            pivot = partition(array,start,end);
            if(pivot>start+1) {
                stack.push(0);
                stack.push(pivot-1);
            }
            if(pivot<end-1) {
                stack.push(pivot+1);
                stack.push(end);
            }
        }
    }

用栈实现队列

我们都知道：栈是遵循先进后出原则的，队列是遵循先进先出原则的。

思路：

先准备两个栈。第一个栈称为stack1，第二个栈称为stack2。

1.模拟队列的进队：当两个栈都为空时，让第一个元素进哪一个栈都可以，此处假设第一个元素进入的是stack1，当第二个元素进入stack1时，无论如何，都是让元素进入stack1。

2.模拟队列的出队：首先，要判断两个栈是否为空，不为空才有出栈的可能。

出栈的情况有两种：

（1）第一种是stack1不为空、stack2为空，首先依次弹出stack1中的元素到stack2中，但是不要把最后弹出的元素压入stack2中，因为它正是“队列”中的第一个元素。

（2）第二种是stack2中的元素不为空时，即使stack1中含有元素，也是先把stack2中的栈顶元素弹出即可，因为它正是“队列”的第一个元素。

如果觉得文字描述不清的话，可以结合下图进行理解：

1.初始：

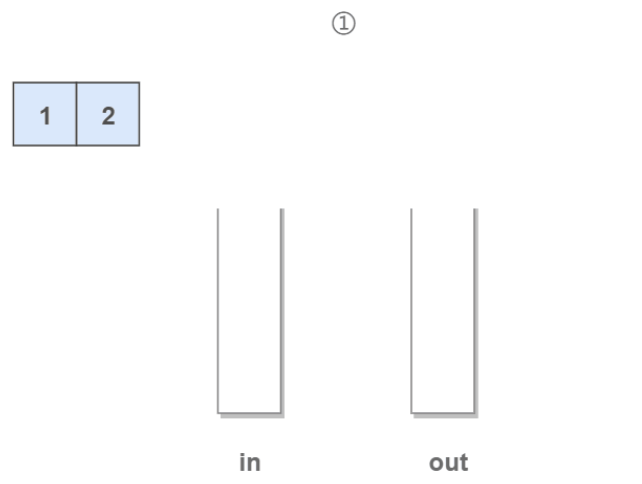
2.有新元素要“入队”：

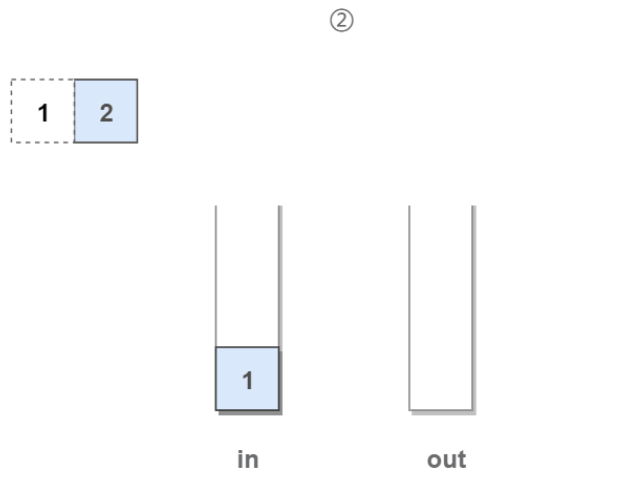
3.再有一个新元素要“入队”：

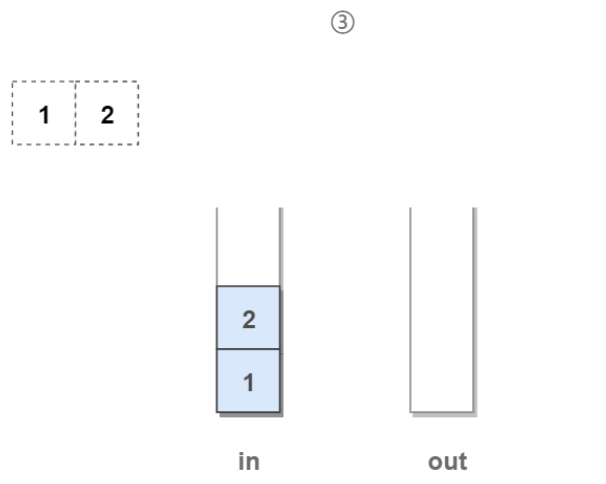
4.此时“出队”操作，先把stack1中的除了最后一个元素依次弹出并依次压入到stack2中：

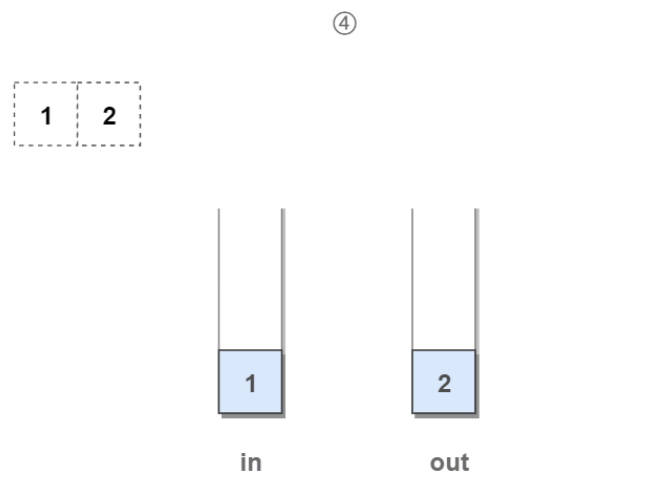
5.如果是求队列中的队头，则stack1中的“1”弹出后要进入到stack2中，此时记录到了元素“1”，返回元素“1”即可：

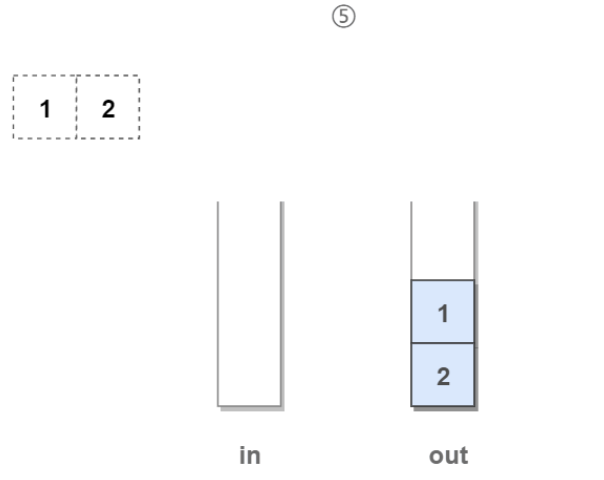
6.此时如果要出队，则直接把stack2中的栈顶元素弹出，它即是队列中的队头元素：

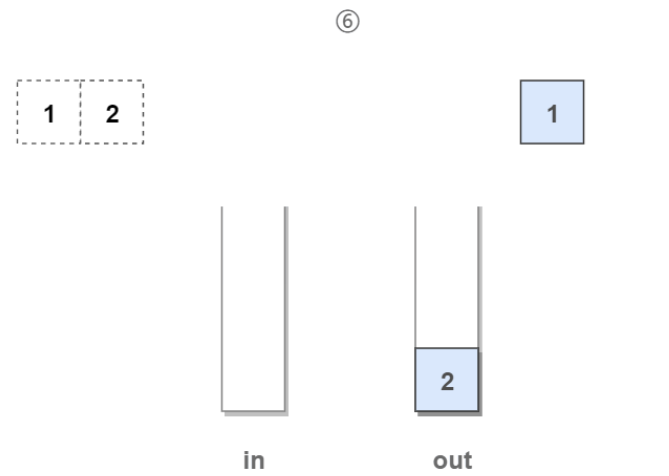
7.相同地，如果stack2不为空，则stack2中的栈顶元素对应的就是队头元素：

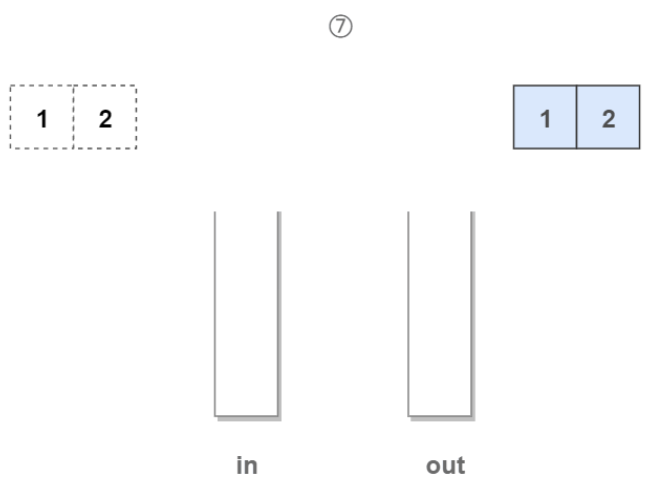
代码如下：

class CQueue {
    Stack<Integer> stack1 = null;
    Stack<Integer> stack2 = null;
    public CQueue() {
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }
    
    public void appendTail(int value) {
        if(stack1==null&&stack2==null) {
            stack1.push(value);
            return;
        }
        stack1.push(value);
    }
    
    public int deleteHead() {
        if(stack1==null&&stack2==null) {
            return -1;
        }
        if(stack1.empty()&&stack2.empty()) {
            return -1;
        }
        if(!stack2.empty()) {
            int ret = stack2.pop();
            return ret;
        }else {
            while(!stack1.empty()) {
                int ret = stack1.pop();
                stack2.push(ret);
            }
            return stack2.pop();
        }
    }
}

时间复杂度：appendTail()函数为O(1) ；deleteHead() 函数在 N 次队首元素删除操作中总共需完成 N 个元素的倒序。

空间复杂度：O(N)最差情况下，栈 stack1 和 stack2 共保存 N 个元素。

反转链表

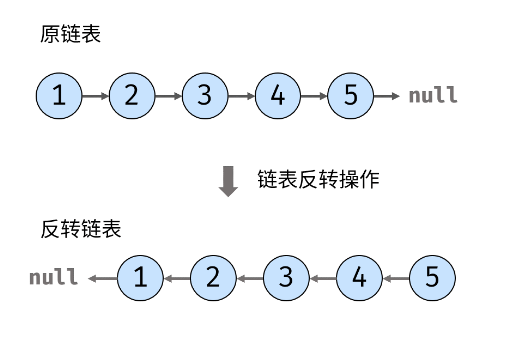
思路：

对于该题，解题的主要方法有两点：第一，如何获取链表当前位置的指针，第二：如何将当前位置的元素的next指针指向前一个元素，所以我们可以创建一个cur指针获得head的一份拷贝，另创建一个prev指针输出原链表的反转。好好理解上面的这句话，能把思路理顺自己进行思考再编码，才能对逐步提高算法能力。

图解：

1.先设置好pre、cur指针：

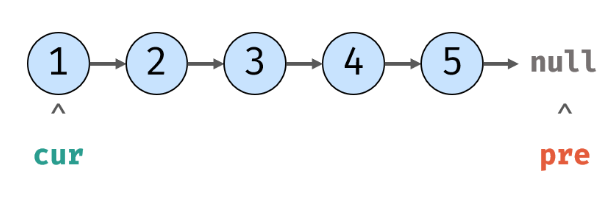
2.设置好tmp指针为cur.next后，再把cur.next设置为pre：

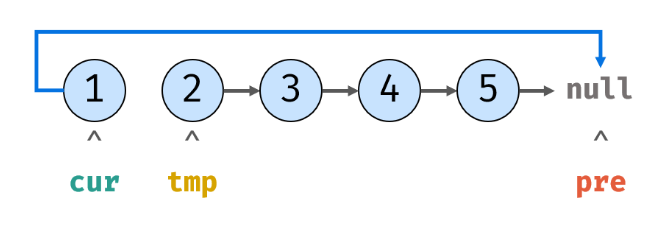
3.此时cur直接指向tmp的内存地址：

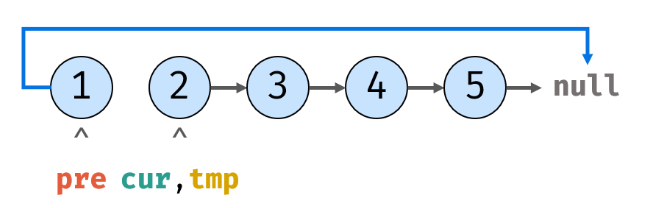
4.tmp移动到cur.next位置后，cur.next再次指向pre：

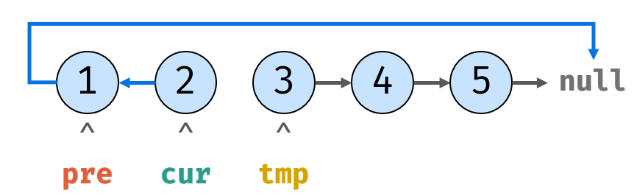
5.重复上述操作，cur指向了tmp的内存地址：

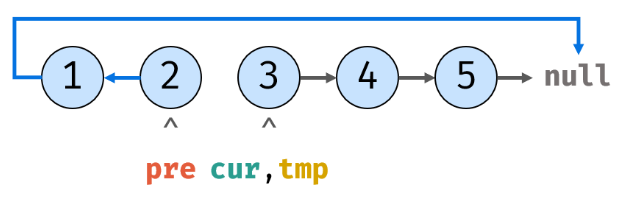
6.tmp设置好为cur.next后，cur.next就指向pre：

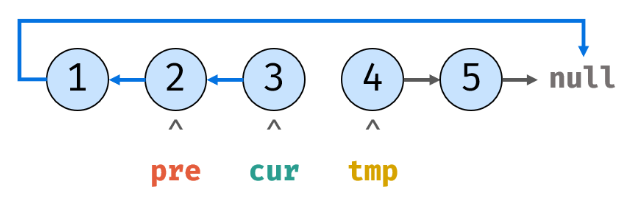
7.重复上述操作，cur指向tmp的内存地址：

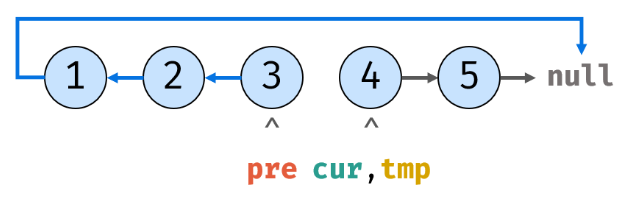
8.tmp再次指向cur.next后，cur.next就指向pre：

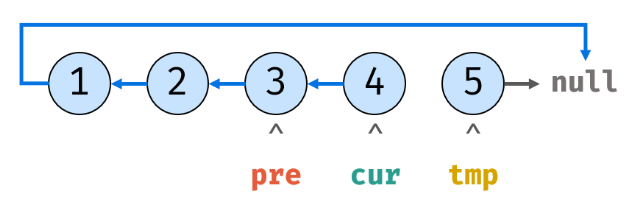
9.pre先指向cur，cur再指向tmp的内存地址：

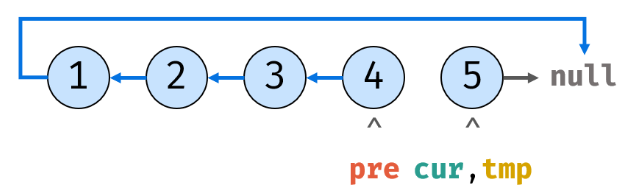
10.tmp此时为cur.next，之后cur.next设置为pre：

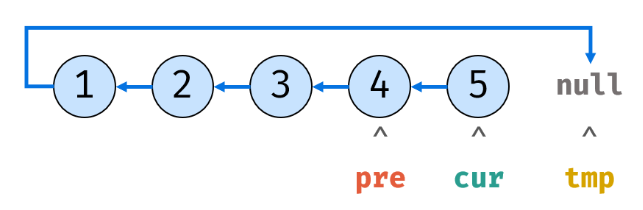
11.pre指向cur的内存地址，cur再指向tmp的内存地址：

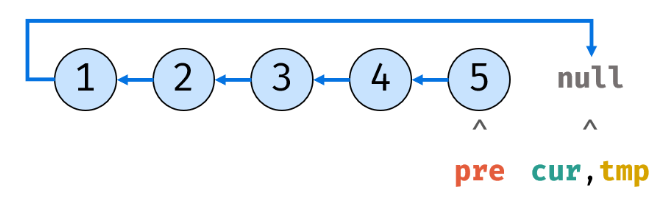
12.最后，链表反转完毕：

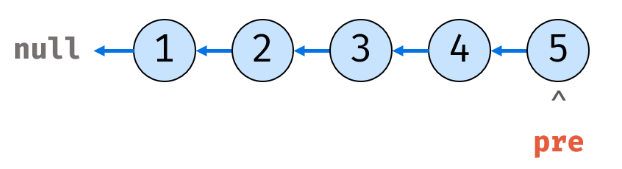
代码如下：

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev =null;
        ListNode cur = head;
        while (cur!=null){
            ListNode next=cur.next;
            cur.next=prev;
            prev=cur;
            cur=next;
        }
        return prev;
    }
}

时间复杂度：O(n)

空间复杂度: O(n)

TopK问题

面试中经常会问到的一道题目：从n个未排序的数中得到的最大的k个数，称为TopK问题。（最小的k个数做法也相似），TopK问题设计到了“堆（优先级队列）”这个数据结构。此处以小根堆为例。若创建堆的时候里面的元素小于K，则入队。继续遍历数组中的元素，若其中有一个数字比堆顶元素大，则于与堆顶元素交换，堆内部对自动调整顺序，下面以找K个最大的数为例。

注意：若找的是前K个最大的数，则要建小根堆；反之要建大根堆。

可以结合图片和文字进行理解：

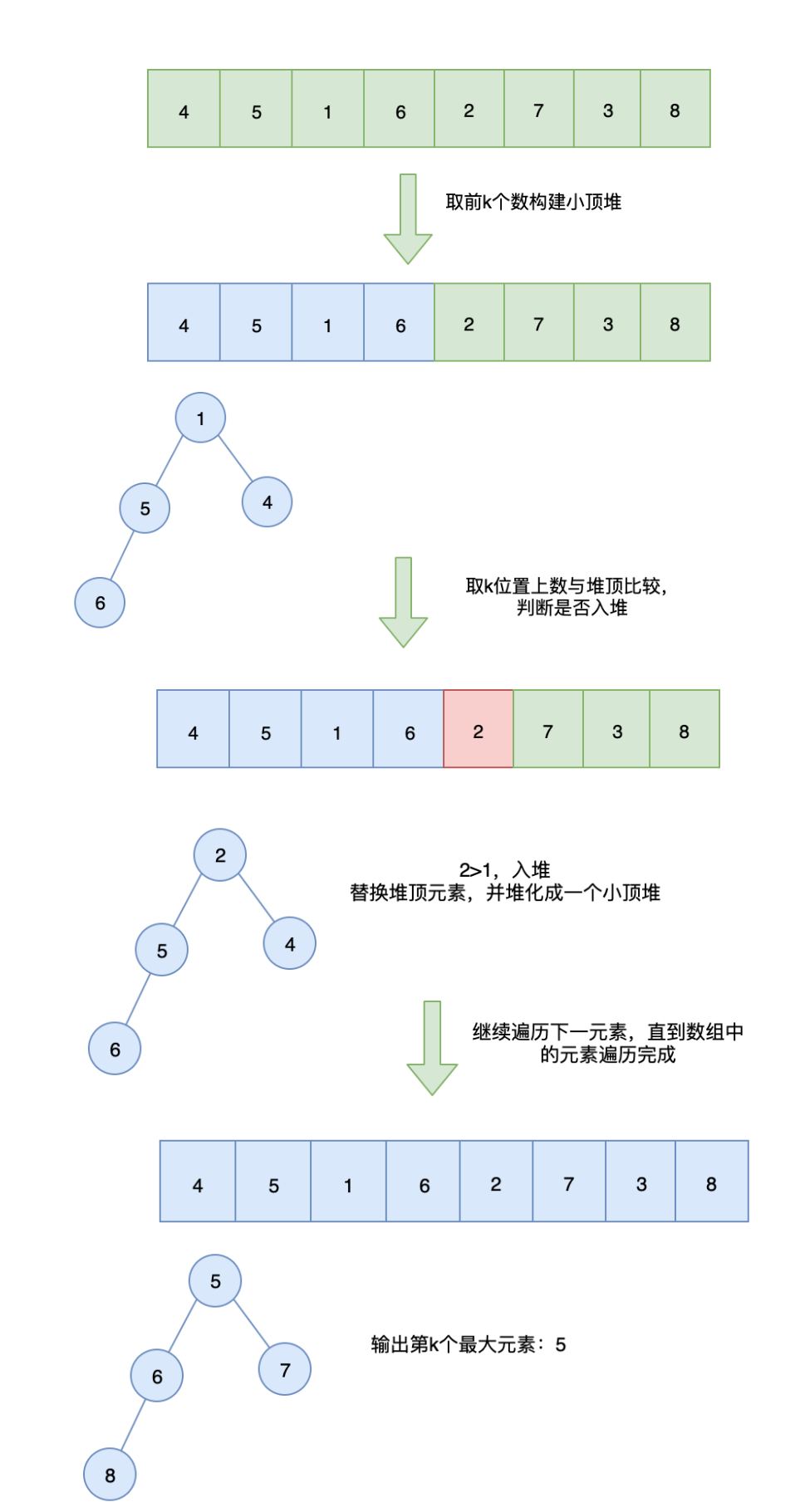
代码如下：

   public static void topk(int[] array,int k) {
      //默认为小根堆
      PriorityQueue<Integer> maxHeap = new PriorityQueue<>(k);
      for (int i = 0; i < array.length; i++) {
            if(maxHeap.size() < k) {
                maxHeap.offer(array[i]);
            }else {
                int top = maxHeap.peek();
                if(top < array[i]) {
                    maxHeap.poll();
                    maxHeap.offer(array[i]);
                }
            }
      }
   }

环形链表

题目描述：给定一个链表，判断链表中是否有环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

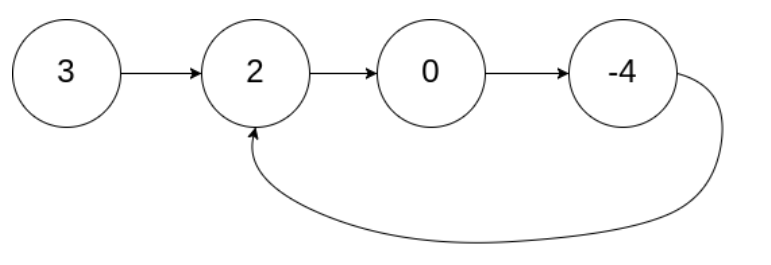
思路：快慢指针：

本方法需要读者对龟兔赛跑算法有所了解。假想“乌龟“和“兔子“在链表上移动，“兔子“跑得快，“乌龟“跑得慢。当“乌龟“和“兔子“从链表上的同一个节点开始移动时，如果该链表中没有环，那么“兔子“将一直处于“乌龟“的前方；如果该链表中有环，那么“兔子“会先于“乌龟“进入环，并且一直在环内移动。等到“乌龟“进入环时，由于“兔子“的速度快，它一定会在某个时刻与乌龟相遇，即套了“乌龟“若干圈。

观察下面代码有个问题：

为什么我们要规定初始时慢指针在位置 head，快指针在位置 head.next，而不是两个指针都在位置 head？

答：因为我们使用的是 while 循环，循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合，如果我们将两个指针初始都置于 head，那么 while 循环就不会执行。因此，我们可以假想一个在 head 之前的虚拟节点，慢指针从虚拟节点移动一步到达 head，快指针从虚拟节点移动两步到达 head.next，这样我们就可以使用 while 循环了。

确定使用快慢指针之后，要注意并理解下面代码中 while 循环的边界条件。即，fast != null 和 fast.next ！= null 缺一不可。在有环的场景下，前者表示当前 fast 指针指向倒数第二个节点的情况；后者表示当前 fast 指针指向倒数第一个也就是最后一个节点的情况。因为 fast 指针每次移动距离为2，所以边界情况有两种。如果 fast 指针每次移动距离是3或者更多，则边界条件会变得更多更复杂，虽然算法速度有所提升，但代码可读性下降明显。所以，这里 fast 指针每次移动2、比 slow 快一个节点即可。

因为 fast 指针肯定比 slow 指针要快，所以显而易见，只用判断 fast 指针是否触达边界即可。

public class Solution {
    public boolean hasCycle(ListNode head) {
        if (head == null || head.next == null) {
            return false;
        }
        ListNode slow = head;
        ListNode fast = head.next;
        while (slow != fast) {
            if (fast == null || fast.next == null) {
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;
        }
        return true;
    }
}

合并两个有序链表

思路：首先，我们设定一个哨兵节点 dum，这可以在最后让我们比较容易地返回合并后的链表。我们维护一个 cur 指针，我们需要做的是调整它的 next 指针。然后，我们重复以下过程，直到 l1 或者 l2 指向了 null ：如果 l1 当前节点的值小于等于 l2 ，我们就把 l1 当前的节点接在 cur 节点的后面同时将 l1 指针往后移一位。否则，我们对 l2 做同样的操作。不管我们将哪一个元素接在了后面，我们都需要把 cur 向后移一位。

在循环终止的时候，l1 和 l2 至多有一个是非空的。由于输入的两个链表都是有序的，所以不管哪个链表是非空的，它包含的所有元素都比前面已经合并链表中的所有元素都要大。这意味着我们只需要简单地将非空链表接在合并链表的后面，并返回合并链表即可。**注意最后返回的是 dum.next **

/**
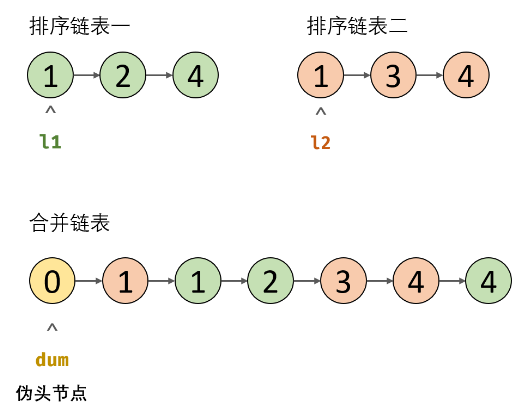
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if(l1==null) {
            return l2;
        }else if(l2==null) {
            return l1;
        }
        ListNode dum = new ListNode();
        ListNode cur = dum;
        while(l1!=null&&l2!=null) {
            if(l1.val>l2.val) {
                cur.next=l2;
                cur=cur.next;
                l2=l2.next;
            }else {
                cur.next=l1;
                cur=cur.next;
                l1=l1.next;
            }
        }
        if(l1==null) {
            cur.next=l2;
        }else {
            cur.next=l1;
        }
        return dum.next;
    }
}

路径总和

题目描述：

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。

说明: 叶子节点是指没有子节点的节点。

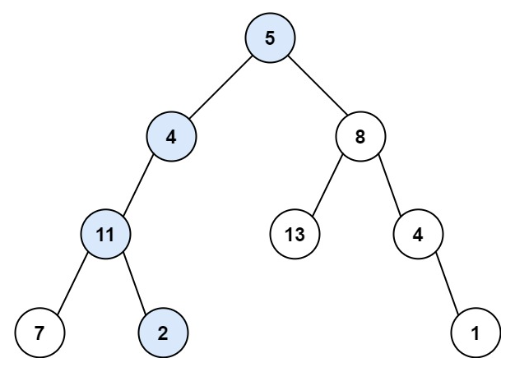
示例: 给定如下二叉树，以及目标和 sum = 22。

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1

返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

思路：

首先，我们要对二叉树的递归比较熟悉，因为是求二叉树中的头结点到叶子结点中的路径总和是否等于targetSum，因此我们不需要设置额外变量，直接在targetSum上操作即可，因为递归栈会帮助我们保留targetSum在递归过程中的值。

因为叶子结点是没有子节点的结点，因此需要先判断targetSum==0&&root.left==null&&root.right==null，这样才能保证到达叶子结点时，并且targetSum==0的情况下返回true。否则继续往左右两边进行递归，直到有满足条件的答案为止。

代码如下：

	public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root==null) {
            return false;
        }
        return process(root,targetSum);
    }
    public boolean process(TreeNode root,int targetSum) {
        if(root==null) {
            return false;
        }
        targetSum-=root.val;
        if(targetSum==0&&root.left==null&&root.right==null) {
            return true;
        }
        return process(root.left,targetSum)||process(root.right,targetSum);
	}

LRU缓存

LRU简介：

LRU是“Least Recently Used”的简写，意思是最近最少使用，是一种缓存淘汰策略，在有限的缓存资源中，淘汰掉最近最久未使用的。例如：缓存最大容纳10000条数据，在添加时，只要数据总数小于等于10000可以随意添加，但是当数据量大于1万时，将旧的数据删除，再添加新的数据；添加时，要将新来的数据添加到最前面。说完来添加，再来说查询，从缓存中获取的数据返回之前，需要将数据移动到最前面，因为获取改数据就代表最近使用了，对于缓存来说，最近这个数据很有可能会被再次使用，所以要移动到最前面。

LRU算法分析：

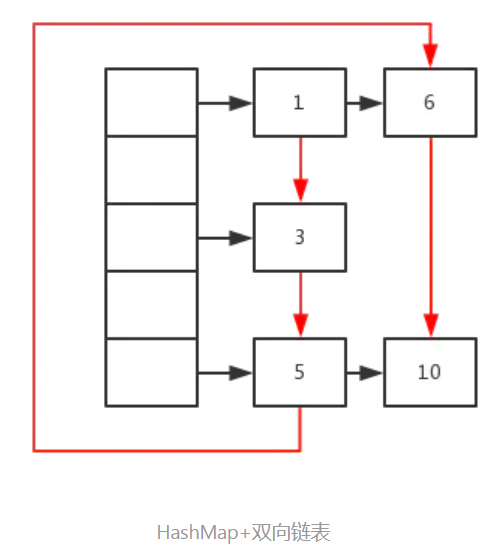
因为缓存具有查询快（时间复杂度必须是O(1)），增加快，删除快的特点。同时，LRU策略分析的数据有新旧之分，新的在最前面，旧的往后放。因此选取数据结构时，要遵循有序的特点。因此可以将HashMap与双向链表结合起来实现LRUCache。Hash表查询效率是O(1)，但是不是有序的，双向链表（此处不是循环链表）有序并且增加与删除都是O(1)，但查询是O(n)，所以两者互相取长补短。

如图所示：

为了让我们了解LRU缓存更加清晰，下面用注释来解释我们所需要完成的LRU缓存的功能：

/* 缓存容量为 2 */
LRUCache cache = new LRUCache(2);
// 你可以把 cache 理解成一个队列
// 假设左边是队头，右边是队尾
// 最近使用的排在队头，久未使用的排在队尾
// 圆括号表示键值对 (key, val)

cache.put(1, 1);
// cache = [(1, 1)]

cache.put(2, 2);
// cache = [(2, 2), (1, 1)]

cache.get(1);       // 返回 1
// cache = [(1, 1), (2, 2)]
// 解释：因为最近访问了键 1，所以提前至队头
// 返回键 1 对应的值 1

cache.put(3, 3);
// cache = [(3, 3), (1, 1)]
// 解释：缓存容量已满，需要删除内容空出位置
// 优先删除久未使用的数据，也就是队尾的数据
// 然后把新的数据插入队头

cache.get(2);       // 返回 -1 (未找到)
// cache = [(3, 3), (1, 1)]
// 解释：cache 中不存在键为 2 的数据

cache.put(1, 4);    
// cache = [(1, 4), (3, 3)]
// 解释：键 1 已存在，把原始值 1 覆盖为 4
// 不要忘了也要将键值对提前到队头

算法设计：

1、如果我们每次默认从链表尾部添加元素，那么显然越靠尾部的元素就是最近使用的，越靠头部的元素就是最久未使用的。

2、对于某一个 key，我们可以通过哈希表快速定位到链表中的节点，从而取得对应 val。

3、链表显然是支持在任意位置快速插入和删除的，改改指针就行。只不过传统的链表无法按照索引快速访问某一个位置的元素，而这里借助哈希表，可以通过 key 快速映射到任意一个链表节点，然后进行插入和删除。

因为面试过程中，面试官大概率会让我们自己去实现一个双向链表来完成LRU缓存的功能，HashMap的话直接使用集合类中现成的即可。

因此结点类为双向链表的结点，有prev和next指针：

class DLinkedNode {
    public int key;
    public int value;
    public DLinkedNode next;
    public DLinkedNode prev;

    public DLinkedNode(int key,int value) {
        this.key=key;
        this.value=value;
    }
}

然后依靠我们的 Node 类型构建一个双链表，实现几个 LRU 算法必须的 API：

class DoubleList {  
    // 头尾虚节点
    private Node head, tail;  
    // 链表元素数
    private int size;
    
    public DoubleList() {
        // 初始化双向链表的数据
        head = new Node(0, 0);
        tail = new Node(0, 0);
        head.next = tail;
        tail.prev = head;
        size = 0;
    }

    // 在链表尾部添加节点 x，时间 O(1)
    public void addLast(Node x) {
        x.prev = tail.prev;
        x.next = tail;
        tail.prev.next = x;
        tail.prev = x;
        size++;
    }

    // 删除链表中的 x 节点（x 一定存在）
    // 由于是双链表且给的是目标 Node 节点，时间 O(1)
    public void remove(Node x) {
        x.prev.next = x.next;
        x.next.prev = x.prev;
        size--;
    }
    
    // 删除链表中第一个节点，并返回该节点，时间 O(1)
    public Node removeFirst() {
        if (head.next == tail)
            return null;
        Node first = head.next;
        remove(first);
        return first;
    }

    // 返回链表长度，时间 O(1)
    public int size() { return size; }

}

先不急于去实现 LRU 算法的 get 和 put 方法。由于我们要同时维护一个双链表 cache 和一个哈希表 map，很容易漏掉一些操作，比如说删除某个 key 时，在 cache 中删除了对应的 Node，但是却忘记在 map 中删除 key。

解决这种问题的有效方法是：在这两种数据结构之上提供一层抽象 API。

可以先实现下面几个函数：

/* 将某个 key 提升为最近使用的 */
private void makeRecently(int key) {
    Node x = map.get(key);
    // 先从链表中删除这个节点
    cache.remove(x);
    // 重新插到队尾
    cache.addLast(x);
}

/* 添加最近使用的元素 */
private void addRecently(int key, int val) {
    Node x = new Node(key, val);
    // 链表尾部就是最近使用的元素
    cache.addLast(x);
    // 别忘了在 map 中添加 key 的映射
    map.put(key, x);
}

/* 删除某一个 key */
private void deleteKey(int key) {
    Node x = map.get(key);
    // 从链表中删除
    cache.remove(x);
    // 从 map 中删除
    map.remove(key);
}

/* 删除最久未使用的元素 */
private void removeLeastRecently() {
    // 链表头部的第一个元素就是最久未使用的
    Node deletedNode = cache.removeFirst();
    // 同时别忘了从 map 中删除它的 key
    int deletedKey = deletedNode.key;
    map.remove(deletedKey);
}

需要注意的是：

当缓存容量已满，我们不仅仅要删除最后一个 Node 节点，还要把 map 中映射到该节点的 key 同时删除，而这个 key 只能由 Node 得到。如果 Node 结构中只存储 val，那么我们就无法得知 key 是什么，就无法删除 map 中的键，造成错误。

上述方法就是简单的操作封装，调用这些函数可以避免直接操作 cache 链表和 map 哈希表，下面我先来实现 LRU 算法的 get 方法：

public int get(int key) {
    if (!map.containsKey(key)) {
        return -1;
    }
    // 将该数据提升为最近使用的
    makeRecently(key);
    return map.get(key).val;
}

Put方法的流程相对复杂，此处用流程图比较清晰Put方法的流程：

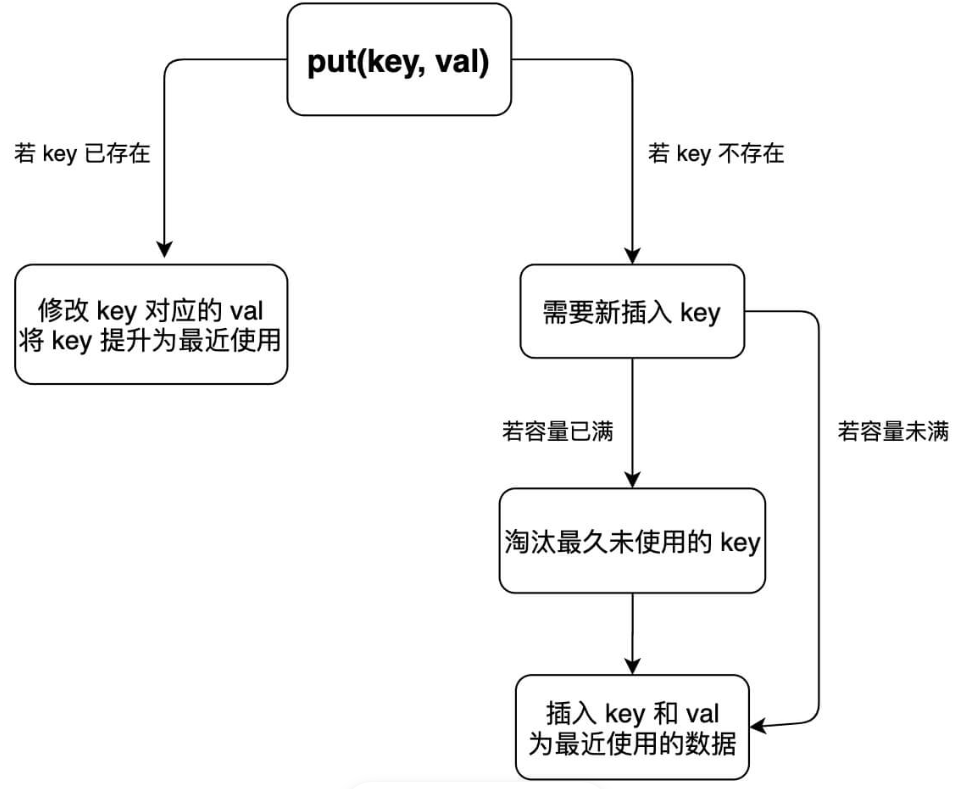
Put流程代码：

public void put(int key, int val) {
    if (map.containsKey(key)) {
        // 删除旧的数据
        deleteKey(key);
        // 新插入的数据为最近使用的数据
        addRecently(key, val);
        return;
    }
    
    if (cap == cache.size()) {
        // 删除最久未使用的元素
        removeLeastRecently();
    }
    // 添加为最近使用的元素
    addRecently(key, val);
}

注意我们实现的双链表 API 只能从尾部插入，也就是说靠尾部的数据是最近使用的，靠头部的数据是最久为使用的。

将上面的代码进行组装，最终的代码为：

class DLinkedNode {
    public int key;
    public int value;
    public DLinkedNode next;
    public DLinkedNode prev;

    public DLinkedNode(int key,int value) {
        this.key=key;
        this.value=value;
    }
}
class LRUCache {
    private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode(0,0);
        tail = new DLinkedNode(0,0);
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            // 添加进哈希表
            cache.put(key, newNode);
            // 添加至双向链表的头部
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode tail = removeTail();
                // 删除哈希表中对应的项
                cache.remove(tail.key);
                --size;
            }
        }
        else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;
            moveToHead(node);
        }
    }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}

了解了上面的过程，我们自己去实现双向链表+哈希表的方式完成了LRU算法，在Java中，有一个内置类型LinkedHashMap等同于是双向链表+哈希表的结构，当面试官不要求我们自己去实现双向链表时，可以直接用LinkedHashMap完成LRU算法的实现：

class LRUCache {
    int cap;
    LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();
    public LRUCache(int capacity) { 
        this.cap = capacity;
    }
    
    public int get(int key) {
        if (!cache.containsKey(key)) {
            return -1;
        }
        // 将 key 变为最近使用
        makeRecently(key);
        return cache.get(key);
    }
    
    public void put(int key, int val) {
        if (cache.containsKey(key)) {
            // 修改 key 的值
            cache.put(key, val);
            // 将 key 变为最近使用
            makeRecently(key);
            return;
        }
        
        if (cache.size() >= this.cap) {
            // 链表头部就是最久未使用的 key
            int oldestKey = cache.keySet().iterator().next();
            cache.remove(oldestKey);
        }
        // 将新的 key 添加链表尾部
        cache.put(key, val);
    }
    
    private void makeRecently(int key) {
        int val = cache.get(key);
        // 删除 key，重新插入到队尾
        cache.remove(key);
        cache.put(key, val);
    }
}

找出数组中的第K大的元素

此处给出四种方法，找出数组中第K大的元素。

方法一：基于元素大小排序

最简单的方法是根据数据量选择不同的排序算法进行排序后，遍历到第K大的数返回即可。当数组长度小于60时，使用插入排序即可；当数组长度大于60时，使用快速排序即可。这种方法过于简单想必各位小伙伴能够解决。

方法二：小顶堆法

二叉堆是一种特殊的完全二叉树，它包含大顶堆和小顶堆两种形式。其中小顶堆的特点是每一个父节点都小于等于自己的两个子节点。要解决这个算法题，我们可以利用小顶堆的特性。

维护一个容量为K的小顶堆，堆中的K个节点代表着当前最大的K个元素，而堆顶显然是这K个元素中的最小值。 遍历原数组，每遍历一个元素，就和堆顶比较，如果当前元素小于等于堆顶，则继续遍历;如果元素大于堆顶，则把当前元素放在堆顶位置，并调整二叉堆（下沉操作）。 遍历结束后，堆顶就是数组的最大K个元素中的最小值，也就是第K大元素。

假设K=5，具体操作步骤如下：

1：把数组的前K个元素构建成堆。

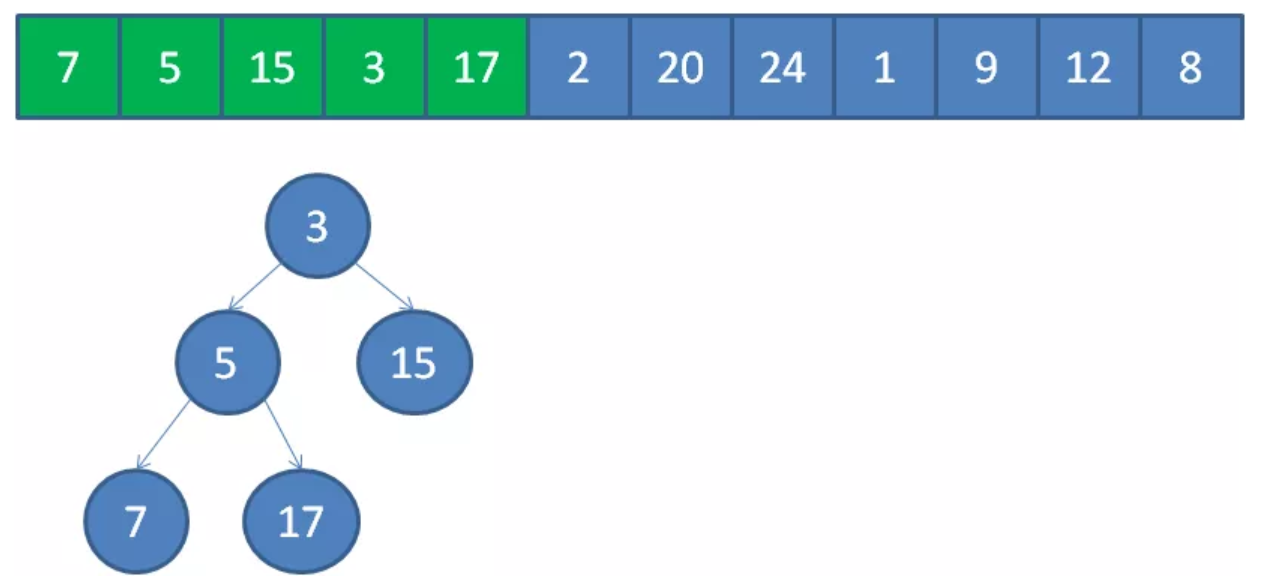
2.继续遍历数组，和堆顶比较，如果小于等于堆顶，则继续遍历;如果大于堆顶，则取代堆顶元素并调整堆。

遍历到元素2，由于2<3，所以继续遍历。

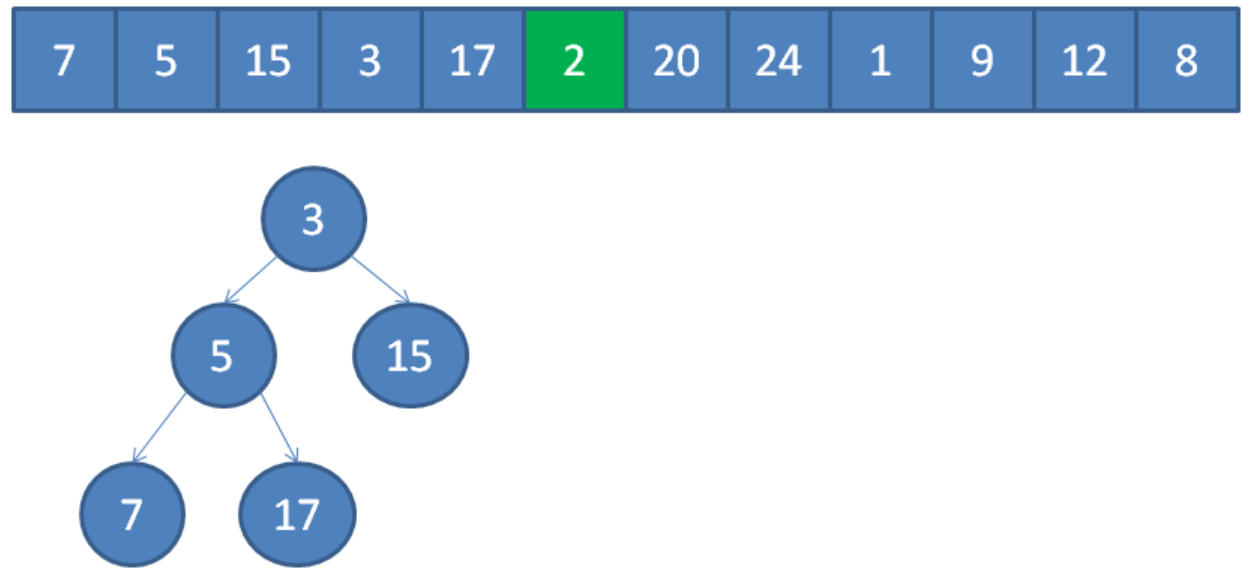
遍历到元素20，由于20>3,20取代堆顶位置，并调整堆。

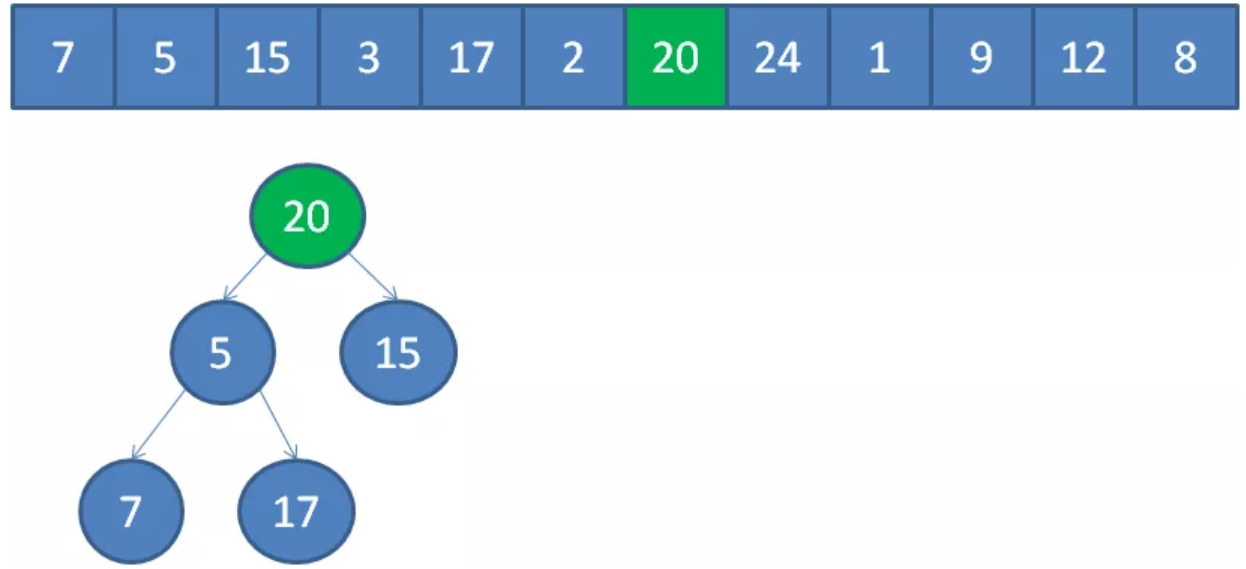
继续调整堆。

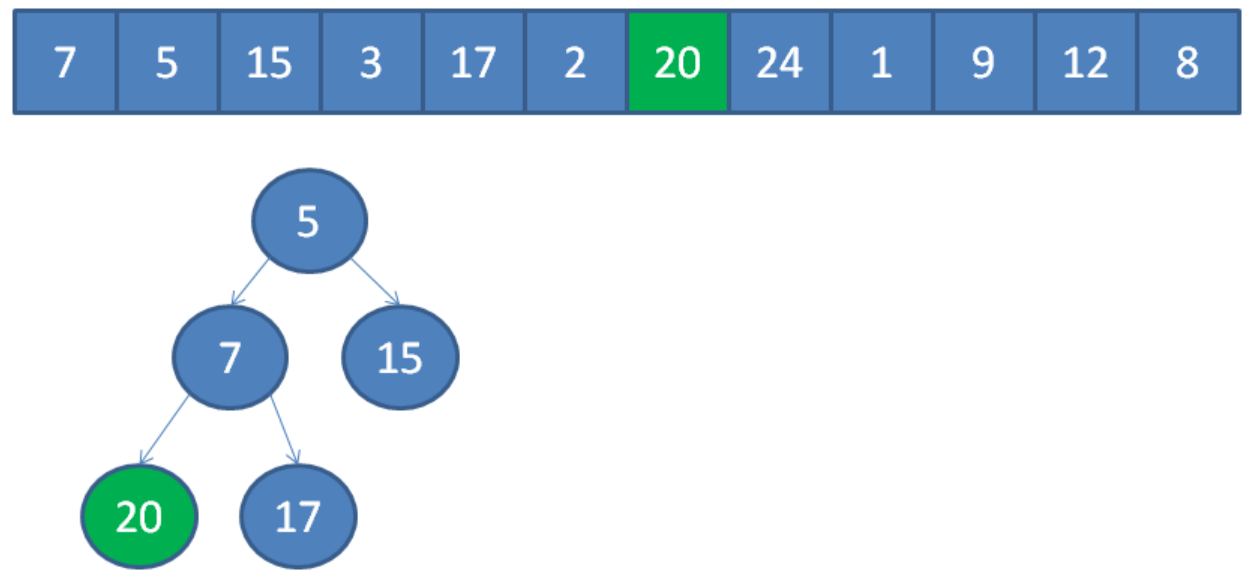
遍历到元素24，由于24>5,24取代堆顶位置，并调整堆。

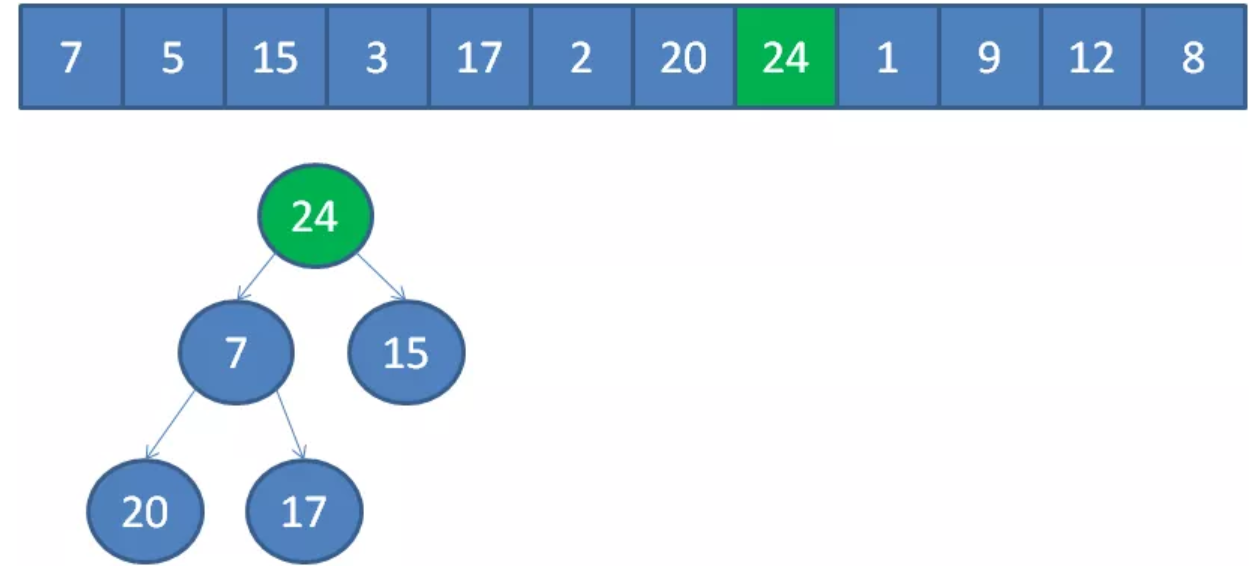
继续调整堆：

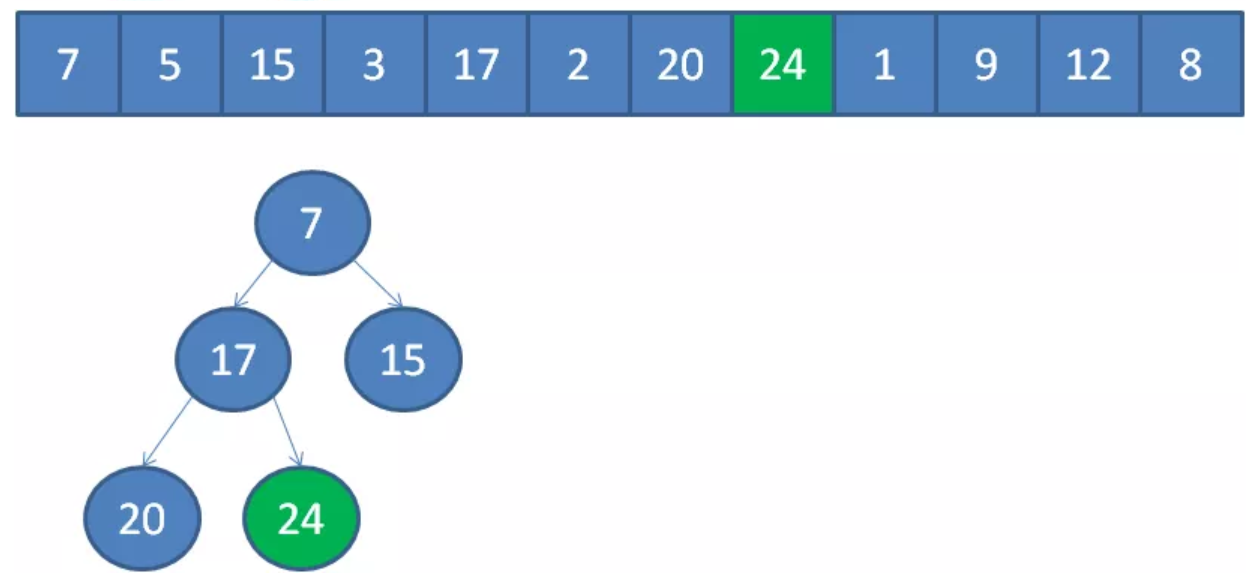
以此类推，我们一个一个遍历元素，当遍历到最后一个元素8时，小顶堆的情况如下：

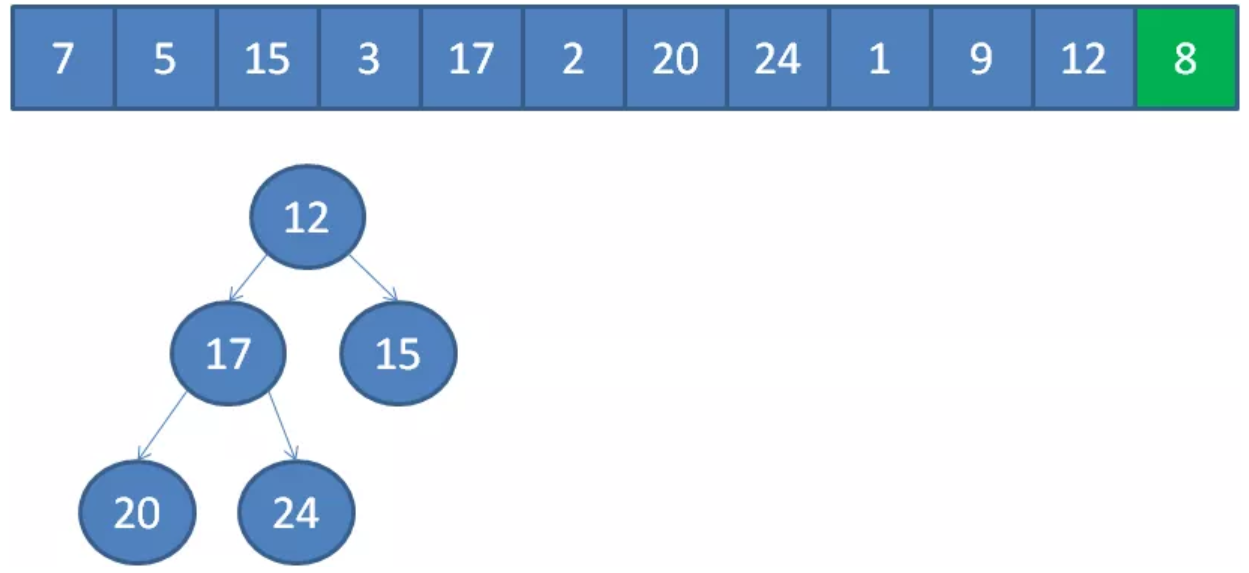
3.此时的堆顶，就是堆中的最小元素，也就是数组中的第K大元素。

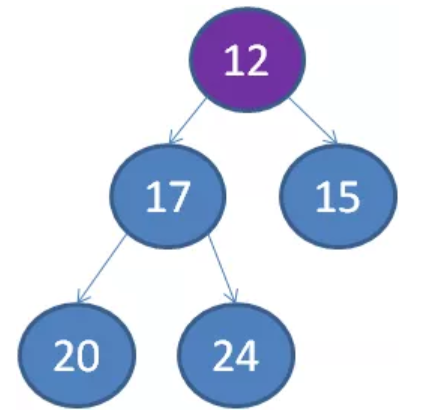
时间复杂度分析：

1.构建堆的时间复杂度是O(K) 2.遍历剩余数组的时间复杂度O(n-K) 3.每次调整堆的时间复杂度是O(logk) 其中2和3是嵌套关系，1和2,3是并列关系，所以总的最坏时间复杂度是O((n-k)logk + k)。当k远小于n的情况下，也可以近似地认为是O(nlogk)。

空间复杂度分析： 刚才我们在详细步骤中把二叉堆单独拿出来演示，是为了便于理解。但如果允许改变原数组的话，我们可以把数组的前K个元素“原地交换”来构建成二叉堆，这样就免去了开辟额外的存储空间。因此空间复杂度是O(1)。

代码如下：

	 /**
     * 寻找第k大元素
     * @param array 待调整的数组
     * @param k 第几大
     * @return
     */
    public static int findNumberK(int[] array, int k) {
        //1.用前k个元素构建小顶堆
        buildHeap(array, k);
        //2.继续遍历数组，和堆顶比较
        for (int i = k; i < array.length; i++) {
            if(array[i] > array[0]) {
                array[0] = array[i];
                downAdjust(array, 0, k);
            }
        }
        //3.返回堆顶元素
        return array[0];
    }

    private static void buildHeap(int[] array, int length) {
        //从最后一个非叶子节点开始，依次下沉调整
        for (int i = (length - 2) / 2; i >= 0; i--) {
            downAdjust(array, i, length);
        }
    }

    /**
     * 下沉调整
     * @param array 待调整的堆
     * @param index 要下沉的节点
     * @param length 堆的有效大小
     */
    private static void downAdjust(int[] array, int index, int length) {
        //temp保存父节点的值，用于最后的赋值
        int temp = array[index];
        int childIndex = 2 * index + 1;
        while (childIndex < length) {
            //如果有右孩子，且右孩子小于左孩子的值，则定位到右孩子
            if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
                childIndex++;
            }
            //如果父节点小于任何一个孩子的值，直接跳出
            if (temp <= array[childIndex])
                break;
            //无需真正交换，单项赋值即可
            array[index] = array[childIndex];
            index = childIndex;
            childIndex = 2 * childIndex + 1;
        }
        array[index] = temp;
    }

    public static void main(String[] args) {
        int[] array = new int[] {7, 5, 15, 3, 17, 2, 20, 24, 1, 9, 12, 8};
        System.out.println(findNumberK(array, 5));
    }

方法三：改写快排方法

我们都知道，快排有个非常重要的Partition过程，它是先选择一个基准后再进行Partition，该过程结束后，能把数组的划分为三部分，比基准小的数都位于最左部分，但是它们是无序的；等于基准的数都位于中间部分；大于基准的数都位于最右部分，它们也是无序的。对快速排序不了解的小伙伴可以查看此文档的快速排序部分，解释的非常清楚。

那要怎么个改写快排呢？

因为只要进行了一次Partition过程，等于基准值的一定是被划分到了中间部分，因此我们可以记录中间部分的起始位置 L 和终止位置 R ，如果 K 是在 L 和 R 范围内，则第K小的数一定是基准值。**网上的帖子一般都是把 Partition 过程修改为左区域是比基准大的，右区域是比基准小的。此处为了不把问题复杂化，还是保持原来的Partition过程。**假设数组的长度为N，因此第K大的数可以转换为求第N-K小的数，就满足了不改变Partition过程也能找到第K小的数的要求。

改写快排主要是不像快排一样，先把基准值调到最终所处的位置然后向左右两边递归。而是假设index（第index小的数）不处于首先所处的基准的范围内后，如果比基准所囊括的L小，则说明该数比基准值要小；反之，如果比基准所囊括的R大，则说明该数比基准值要大。

需要注意两个地方：

1.基准的选取是随机的：int pivot = arr[L + (int) (Math.random() * (R - L + 1))];，不像快速排序一样选取一定选取最左边的数最为基准。

2.Partition过程返回的是一个数组，该数组只有两个元素，0下标的元素是基准所在的最左的边界下标，1下标的元素是基准所在的最右的边界下标。在process中，当index在基准的左边时，只需要递归数组左边的数即可，不用递归右边的，因此用了if-else作了判断。同样地，当index在基准的右边时，只需要递归数组右边的数即可，不用递归左边的。

代码如下：

	// arr 第k小的数
	// process2(arr, 0, N-1, k-1)
	// arr[L..R]  范围上，如果排序的话(不是真的去排序)，找位于index的数
	// index [L..R]
	public static int process(int[] arr, int L, int R, int index) {
		if (L == R) { // L = =R ==INDEX
			return arr[L];
		}
		// 不止一个数  L +  [0, R -L]
		int pivot = arr[L + (int) (Math.random() * (R - L + 1))];
		int[] range = partition(arr, L, R, pivot);
		if (index >= range[0] && index <= range[1]) {
			return arr[index];
		} else if (index < range[0]) {
			return process(arr, L, range[0] - 1, index);
		} else {
			return process(arr, range[1] + 1, R, index);
		}
	}

	public static int[] partition(int[] arr, int L, int R, int pivot) {
		int less = L - 1;	
		int more = R + 1;
		int cur = L;
		while (cur < more) {
			if (arr[cur] < pivot) {
				swap(arr, ++less, cur++);
			} else if (arr[cur] > pivot) {
				swap(arr, cur, --more);
			} else {
				cur++;
			}
		}
		return new int[] { less + 1, more - 1 };
	}

	public static void swap(int[] arr, int i1, int i2) {
		int tmp = arr[i1];
		arr[i1] = arr[i2];
		arr[i2] = tmp;
	}

时间复杂度为O(N)，因为此方法只是递归了一边，而快速排序的递归是向左右两边递归的，因此时间复杂度一定比快排快，对比方法一和方法二的时间复杂度优秀了很多。

方法三使用快排改进的方法有一个小问题，在选取基准的时候是随机选取的，如果运气不好选取到的基准是数组中的最大或者最小值时，跟快排一样，时间复杂度是最差情况下的。因此方法四使用bfprt算法应运而生。

方法四：bfprt算法解决找出数组第K大的元素

可能许多小伙伴对bfprt算法不太了解，这个算法就是专门来解决在一个数组中寻找第K小或者第K大的数。

bfprt算法介绍

BFPRT算法又叫中位数的中位数算法，主要用于在无序数组中寻找第K大或第K小的数，它的最坏时间复杂度为O(n)，它是由Blum，Floyd，Pratt，Rivest，Tarjan提出，它的思想是修改快速选择算法（快排）的主元选取方法，提高在最坏情况下的时间复杂度。

bfprt的具体方法：

BFPRT算法主要由两部分组成：快排和基准选取函数。基准选取函数就是中位数的中位数算法的实现，具体来说--就是讲快排的基准选取策略进行了优化，改为每次尽可能的选择中位数作为基准。

所以说算法的核心就是通过基准选取函数找一个合理的划分值，然后就是快排的Partition过程，判断等于区域（利用区域的下标进行判断）是否命中k，否则向两边其中一边递归。

bfprt的具体实现：

bfprt解法和常规解法唯一不同的就是在number的选取上，其他地方一模一样，所以我们只讲选取number这一过程。

第一步：我们将数组每5个相邻的数分成一组，后面的数如果不够5个数也分成一组。

第二步：对于每组数，我们找出这5个数的中位数，将所有组的中位数构成一个median数组（中位数数组）。

第三步：我们再求这个中位数数组中的中位数，此时所求出的中位数就是那个number。

第四步：通过这个number进行partation过程，下面和常规解法就一样了。

接下来我们分析一下为什么bfprt算法每次选number的时候都能够在数组的中间位置。

有了上面的基础之后，我们可以直接利用bfprt算法解决问题了，对于方法三的快排改进问题，bfprt算法只是在选取基准值的时候进行了优化，它能够保证选取的基准值，如果是最坏情况下，一定是至少有3N/10的元素比基准值大，至少有7N/10的元素比基准值小。

此处只对bfprt算法作简单了解来解决本题，如有兴趣对bfprt算法更细一步的学习，可以参考《算法导论》，里面有关于bfprt算法的证明以及实现的全部过程。

最终使用bfprt算法解决问题的代码如下：

	// arr[L..R]  如果排序的话，位于index位置的数，是什么，返回
	public static int bfprt(int[] arr, int L, int R, int index) {
		if (L == R) {
			return arr[L];
		}
		// L...R  每五个数一组
		// 每一个小组内部排好序
		// 小组的中位数组成新数组
		// 这个新数组的中位数返回
		int pivot = medianOfMedians(arr, L, R);
		int[] range = partition(arr, L, R, pivot);
		if (index >= range[0] && index <= range[1]) {
			return arr[index];
		} else if (index < range[0]) {
			return bfprt(arr, L, range[0] - 1, index);
		} else {
			return bfprt(arr, range[1] + 1, R, index);
		}
	}

	// arr[L...R]  五个数一组
	// 每个小组内部排序
	// 每个小组中位数领出来，组成marr
	// marr中的中位数，返回
	public static int medianOfMedians(int[] arr, int L, int R) {
		int size = R - L + 1;
		int offset = size % 5 == 0 ? 0 : 1;
		int[] mArr = new int[size / 5 + offset];
		for (int team = 0; team < mArr.length; team++) {
			int teamFirst = L + team * 5;
			// L ... L + 4
			// L +5 ... L +9
			// L +10....L+14
			mArr[team] = getMedian(arr, teamFirst, Math.min(R, teamFirst + 4));
		}
		// marr中，找到中位数
		// marr(0, marr.len - 1,  mArr.length / 2 )
		return bfprt(mArr, 0, mArr.length - 1, mArr.length / 2);
	}

	public static int getMedian(int[] arr, int L, int R) {
		insertionSort(arr, L, R);
		return arr[(L + R) / 2];
	}

	public static void insertionSort(int[] arr, int L, int R) {
		for (int i = L + 1; i <= R; i++) {
			for (int j = i - 1; j >= L && arr[j] > arr[j + 1]; j--) {
				swap(arr, j, j + 1);
			}
		}
	}